部活から帰ると
部活帰りにカラオケに行こうという約束は白紙になってしまった。
約束していた友達が来れなくなったのである。
ひとりで歌う気分でもなかったので予定よりもだいぶ早い帰宅となった。
「ただいまー」
「・・・」
返事がない。この時間であれば母も弟も家にいるはずである。
靴を脱ごうと片足立ちで足先に手を伸ばしたとき
「おかえりー」(ドンッ)
母親の返事とその裏で鈍い音が聞こえた。おそらく冷蔵庫が閉まる音だ。
靴を脱いでリビングへ入るとそこに弟もいた。
キッチンから母が顔をのぞかせる。
「あれ?もっと遅くなる予定じゃなかった?」
「友達が急にこれなくなっちゃって」
ふと弟に目をやるとどこかいつもと様子が違う。
いつもならソファに寝っ転がってゲームをしているのに今はただ机の横で棒立ちになっている。
こちらの視線に気づいたのかちらっと目が合ったと思えばすぐに視線をそらされる。
(何か隠してる)
そう直感した次の瞬間には私は冷蔵庫に向かって歩いていた。
「ばれたか~」
母があきらめたようにそうつぶやく。
冷蔵庫の中には少し大きめの“正方形のいちごのショートケーキ”があった。

母曰く、私と父が帰ってくる前に弟と二人で分けて食べるつもりだったとのこと。
(お母さん、本当にダイエットするつもりあるのかな)
「3人で食べましょ!ほら、勉強するには糖分も必要だし」
「4等分してお父さんに一つ残してあげたら?」
「『ダイエットするんじゃなかったの?』とかなんとか言われるから内緒」
「適当なこと言って私まで巻き込んで」
「ん~、三角形にわけるのは難しそうね」
私の話は全く聞かずさっそく母はショートケーキを縦長に切り分けていた。
(・・・ん?三角形に均等に分けるのってできないの?)
正方形のケーキを同じ大きさの3つの三角形に切り分ける。
そんな風に切り分けられないことを母は直感的に感じていたようである。
私も少し考えたけれども思いつかない。
気づけばテーブルの上にはケーキと紅茶が用意されていた。
「お姉ちゃんどうして難しい顔してるの?」
「この顔はなんかの問題を考えてるときの顔よ」
「なんでわかるの」
「何年あなたのお母さんやってると思ってるの」
(当たっているから反論できない)
「しかしそういうところはお父さん譲りね」
ケーキを食べ始めるやいなや、弟が今日学校であったことを話し始めた。
そんなこんなで問題を考えるのを中断し、続きはまたお風呂のときにでも考えることした。
父の書斎にて
結局お風呂の中でもいいアイデアは思い浮かばなかった。
おかげで危うくのぼせるところだった。
髪を乾かし終えたら父にちょっと聞いてみよう。
難しい話にはコーヒーを
書斎の扉は開いているが一応ノックする。
(トントン)
「ん?」
「お風呂あいたよ」
「わかった。ありがとう」
「・・・」
「他にも?」
「実は気になる問題があって」
「おっと、それならまずはコーヒーを」
父がコーヒーをいれに行った。
しまった。砂糖抜きだと伝えるのを忘れてしまった。
ただでさえ甘ったるいケーキを食べてしまったのに。
父の机に寄ってみる。どうも小テストの採点をしているようだ。
復習がてら自分も解き方を考えてみる。
このぐらいなら暗算でもいけそうだ。
そうこうしているうちに父が書斎に戻ってきた。
「で、気になってる問題って?」
「正方形をいくつかの三角形に分割したいんだけど条件があって」
そう言って書斎にあるホワイトボードに条件を書き出した。
- 奇数個に分割すること(3個、5個、7個とか)
- どれも同じ大きさに分割すること
「条件はこの二つ」
「ほう」
「だけどうまく分ける方法が見つからなくって」
「なるほどね」
「そもそもできる証拠もないし」
「分割する条件を書き直してみようか」
そういって父はホワイトボードにこう書いた。
- 切り分けたそれぞれパーツは三角形にすること。(形はちがってもいい。)
- 三角形の面積はすべて等しいようにすること。
- 奇数個に切り分けること。
「これはモンスキーの定理だね」
「もんすきー?」
モンスキーの定理(偶数はOK?でも奇数はNG?)
聞きなれない言葉が出てきた。きっと人名かな。
「書いてみると」
そう言って父はホワイトボードに定理の内容と思しき文章を書き始めた。
衝撃が走った。
奇数個だと不可能!?
偶数個なら簡単なのに!?
「やっぱりびっくりした?」
「できないんだ・・・できないことが証明されてるんだ・・・」
「面白いよね。もう一つ面白いことに、僕がこの定理を初めて知ったのは同じく高校生のときだったよ」
「お父さんの高校時代とかあんまり聞いたことないな・・・」
「普通の高校生とはいろいろ違ったけど結構青春してたよ」
「へ~」
「それはさておき、偶数個なら簡単に分けられるのはわかるよね」
「こんな感じだよね」
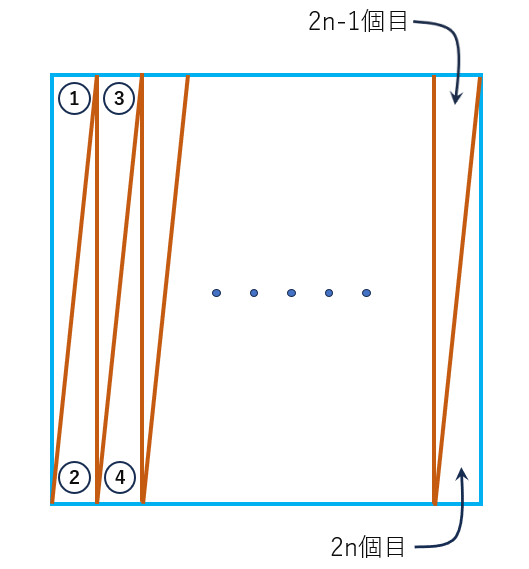
ホワイトボードに図を描いてみた。
「偶数個は簡単だね。ところが奇数個になった途端これが不可能になる。」
ある補題
「簡単に証明できるの?」
「ん~、詳細なところまで議論しようとすると『付値(ふち)』という代数学のツールを使うことになる」
「付値?」
「うん。大学で代数学を勉強すると出会う概念。」
「代数学って聞いたことはあるけど・・・」
「まあ、ある事実を認めれば証明の流れはつかめると思う。」
「ある事実って?」
- どんな直線を引いてもその直線上の点は高々2色である。
- 3頂点の色がすべて異なる三角形の面積は(
とか
みたいに)奇数分の1にならない。
「この補題の証明に付値が必要になってくる」
「その通り。まずはこの補題のイメージを掴んでみよう。」
父は次にこんな図を描いた。
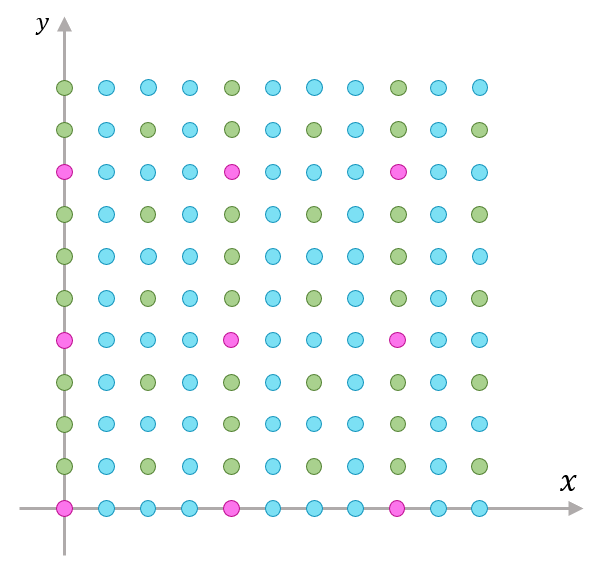
「こんな感じかな」
「補題1にかいてある“3色の塗分け”がこれ?」
「そう。ほんとはもっとびっちり点が埋まってるから白色のところなんてないけど」
「ひとつめの条件は『どんな直線を引いてもその直線上の点は高々2色』だっけ」
「具体的に言うと、どんな直線を引いても必ず次の6パターンしかない」
- 直線状に青色の点しかない
- ーーーー緑色の点しかない
- ーーーー赤色の点しかない
- ーーーー青と緑の点しかない
- ーーーー緑と赤の点しかない
- ーーーー赤と青の点しかない
「要するに3色すべてが一直線上に存在することはないってこと・・で合ってる?」
「うん、その通り。」
sketch of proof
「補題1と今から書く補題2を使えばモンスキーの定理の証明ができあがる」
「えーっと、モンスキーの定理とのつながりはこう?」
- 正方形を奇数個の三角形に分割にする(議論の出発点)
- 正方形の三角形分割には必ず3頂点の色がすべて異なる三角形が含まれる(補題2)
- 3頂点の色がすべて異なる三角形の面積は奇数分の1になることはない(補題1ー2)
- よってモンスキーの定理が示されたことになる
「そうだね。」
「補題1は証明抜きで事実だと認めることにしてるからあとは補題2だけ示せばOKってことか」
「補題2の証明を追うために正方形の三角形分割の図を描いてみるよ」
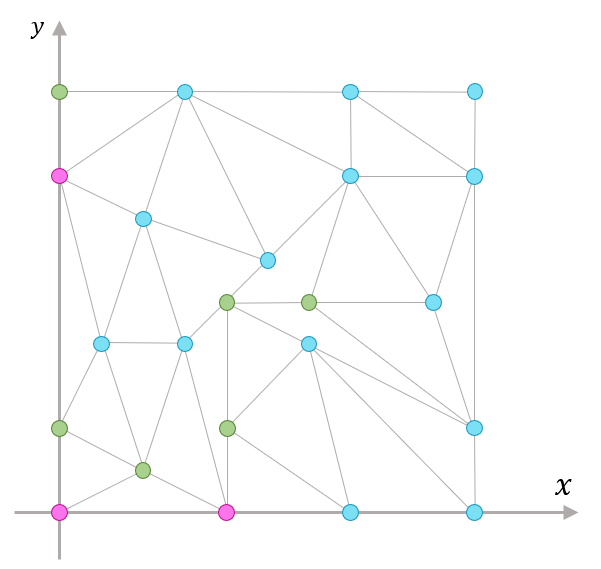
「図描くの早いね」
「職業病だよ」
「え?地雷?」
「まあそれはさておき、こんな感じで正方形を三角形分割したときに・・・」
「“3頂点の色がすべて異なる三角形が奇数個含まれる”ってことを示す」
「注目すべきは両端が赤と青の線分」
「赤と青の線分?っていうと、この図だと5本?」
私もホワイトボードに向かって手を伸ばす。
両端が赤と青の線分を黄色で目立たせた。
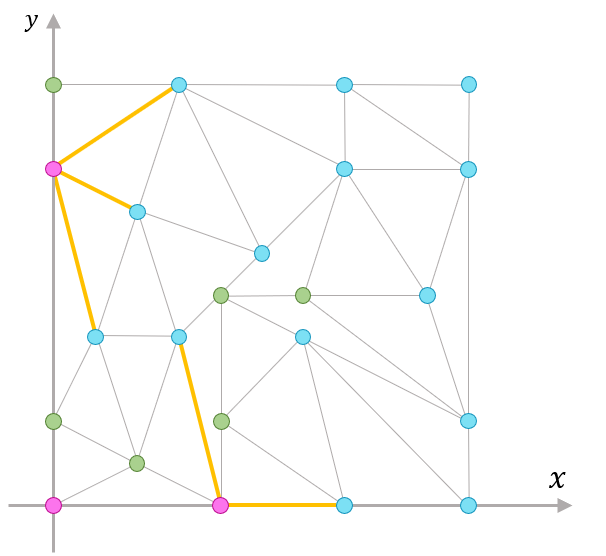
「この図だと黄色で塗ったこの5本だね。」
「まず軸、正方形の一番下の辺にある赤青線分は必ず奇数本になることはわかる?」
「今の図だと赤青線分、黄色の線分は確かに1本だけれど」
「どんな風に三角形分割をしても軸上の赤青線分は奇数本になる」
どうしてだろう。
お父さんが私に問いかけているということは必要なヒントはすでに教えてくれてるはず。
使えるヒントといえば補題1。
補題1は2つの内容からなってたよね。
補題1-2は三角形の面積の話だから直接は関係なさそう。
じゃあ補題1ー1かな?
「補題1-1から軸上の点はすべて赤か青」
父の表情に変化は特にない。ポーカーフェイスに徹しているようだ。
原点は赤色、座標は青色、その途中は赤か青の点しかなくて・・・・
そうか!赤から始まって青で終わるから偶数本はありえないのか!
きっと帰納的に考えれば説明できる。
「原点は赤色、点は青色でこの間に三角形の頂点がなければ赤青線分は当然1本」

「三角形の頂点が一つ増えても、例えば青色の点が増えても赤青線分の本数は変わらず1本」

「また三角形の頂点が一つ増えるとする。今度は青と青の点の間に赤色の点が増えたとすると赤青線分は3本」

「こんな感じで点を増やしていくことでどんな三角形分割の状態も構成できる。そして大事なことは点を増やしたときには赤青線分が増えないか、またはちょうど2本だけ増えるってこと?」
「その通り!」
今までの議論をまとめてみると
- 原点と点
以外に三角形の頂点がなければ赤青線分は1本しかない。
- 最初の三角形分割と同じ状態になるまで原点と点
の間に赤と青の点を追加していく。
- 点を追加したとき、赤青線分は追加する前と比較して全く増えないか、またはちょうど2本増えるかのどちらか。
- 1~3より、赤青線分は最初の1本の状態から偶数本しか増えない。つまり赤青線分は奇数本ということになる。
「いい感じ。この事実を補題1の系として記録しておこう。」
さらりと書き終え父はこう続けた。
「いよいよ本題の補題2の証明に移ろう。」
「例として描いた三角形分割の図をもう一度見てみる。」

「この三角形分割は三角形同士がくっついてるからこんな感じでばらしてやる」
「このとき、正方形内部の赤青線分以外は必ず偶数本となる。」
「二つの三角形の共通の辺だから分割したら2倍の本数になる。だから偶数本。」
「そう。上の図だと正方形内部の赤青線分は8本になるね。」
「正方形の外周の赤青線分ついて考えてみると、軸と重なっているところは奇数本だね。」
「これはさっき私が示した系だよね。」
「そしてそれ以外の外周は赤緑の線分、青緑の線分、青だけの線分のどれかしかない」
「これは補題1-1、どの直線上も高々2色の点しか存在しないことから分かるね」
「ということは、赤青線分は全部で奇数本存在することになる」
「三角形分割をばらして考えた上の図では9本」
「もし仮に“3頂点の色がすべて異なる三角形が偶数個だったとしたら”」
「・・・そっか。赤青線分は全部で偶数本になっちゃうのか」
「そう。三角形の周の赤青線分が奇数本になるのは三角形の頂点の色がすべて異なるときだけだからね」
「以上から頂点の色がすべて異なる三角形は奇数個存在すること、つまり補題2が示されたことになるってわけか」
コーヒーも飲み終えて
「と、まあ証明の流れはこんな感じ」
「どうやったらこんな証明が思いつくんだろう」
「すごいよね」
「補題1の証明は難しいの?」
「ん~、付値を使った議論を説明するにはちょっと準備と時間がかかるかな」
「興味はあるけど宿題やらなきゃいけないからまた今度教えて」
「いつでも。これを読んでる人には僕から説明しておくよ」
「“これ”?」
「いやなんでもない。こっちの話」
「指示語ばっかり。ともかくありがとう。面白かった。」
「こちらこそ。いい反応が見れてよかったよ。ところでどうしてこの問題思いついたの?」
「あっ」
しまった。問題に気を取られてばかりいた。
「えーっと・・・」
洗いざらい話した。
父と同じく咄嗟に嘘をつけない性格であることは自覚していたから。
「ダイエットするんじゃなかったの?」
「内緒だからね」
「・・・僕も食べたかった」
「私がばらしたこと内緒だからね」
「僕も・・・」
二人ともコーヒーカップはとっくに空になっていた。
カップを二つ持って私は書斎から出た。
そういえば、ずいぶん話し込んでしまったけれどお風呂はまだあったかいのかな。
・・・温めなおしといてあげるか。
バトンタッチ
部屋を出る娘の後ろ姿をみて改めて子供の成長の速さに驚かされる。
ついこの間までは九九の練習に付き合っていたぐらいなのに。
「さてと・・・」
みなさん。どうでした?
四角いケーキを三角形にわけるだけ、たったそれだけのことなのに、同じ大きさで奇数個に切り分けることが不可能だなんて意外な結果だったんじゃないでしょうか。
次の記事ではもう一歩踏み込んで付値に関する議論と平面上の点を3種類に“うまく”分類する方法(赤・青・緑の塗分け方)について話します。
本当は今すぐ話したいのですが・・・小テストの採点を終わらせないといけないので今日はこのあたりで。
それにしても、僕もケーキ食べたかったな。